Lo scopo di una simulazione in un esperimento è quello di darci a priori informazioni sul segnale da misurare, sulla base unicamente della teoria e di precedenti dati sperimentali. In questo modo è possibile:

• ottimizzare l'apparato sperimentale per il range di segnale che ci si aspetta;
• calcolare il rapporto segnale rumore aspettato;
• scegliere i parametri di acquisizione dei dati;
• trovare l'oggetto da studiare maggiormente compatibile con la strumentazione in uso.

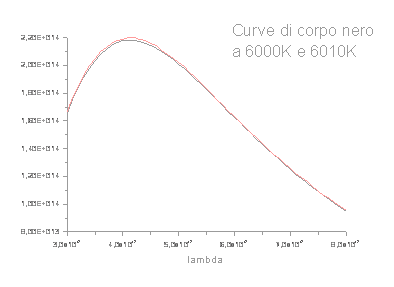
Ovviamente si faranno delle ipotesi semplificative e delle approssimazioni: in questo caso si assume che lo spettro di luce emesso da una stella sia di corpo nero. A temperature differenti saranno associate planckiane differenti, come mostra il grafico.

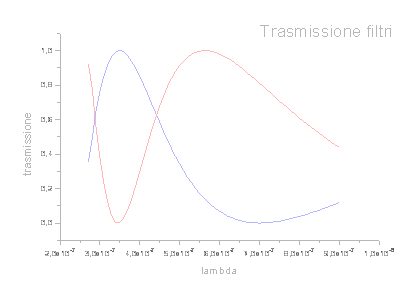
Osservando la stella con un filtro centrato sul blu, si vedrà quindi un aumento di segnale quando la temperatura cresce: lo stesso accadrà per il canale rosso. Il segnale totale sarà l'integrale della curva sulle frequenze. occorre però prima considerare l'effetto dei filtri. Moltiplicando la planckiana per la risposta del filtro e integrando sul range di frequenze in cui il segnale non è nullo, si ottiene il flusso totale. Si calcolano così 4 dati: Ro, Bo, dR e dB, rispettivamente il flusso medio nei due canali rosso e blu e l'ampiezza delle oscillazioni. Si può ora costruire la serie temporale, attraverso una funzione del tipo:

R = Ro + dRcos(wt) ;  B = Bo + dBcos(wt).

Ovviamente si tratta sempre di una approssimazione di ordine zero, anche se abbiamo verificato che è consistente con la teoria, ad esempio l'andamento del flusso con la temperatura alla quarta, oppure la relazione lineare dL/L≈dT/T.

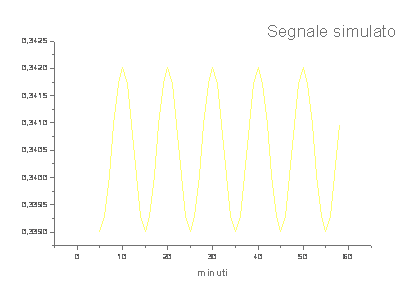
La misura è differenziale: S = (R-B)/(R+B); con questo accorgimento è possibile diminuire sensibilmente l'incidenza della variazione della trasparenza atmosferica, dei movimenti dell'oggetto nel campo, etc. Si riduce anche l'effetto della scintillazione, ma poichè quest'utlima ha un comportamento cromatico, la misura differenziale non potrà eliminarla del tutto. A fianco è mostrata la serie temporale così ottenuta. Ora bisogna aggiungere il rumore.

Simulazione del rumore di scintillazione.

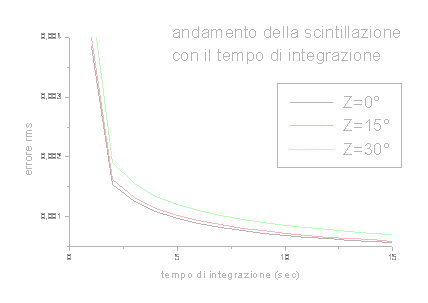
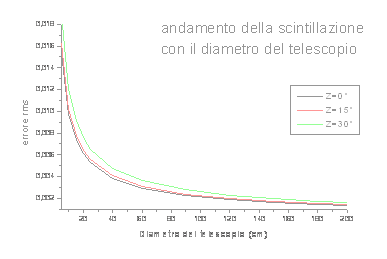
La scintillazione è causata dalla turbolenza atmosferica. E' caratterizzata da uno spettro piatto, almeno fino ad una certa frequenza di taglio υ=V/πD, in cui V è la velocità del vento perpendicolarmente alla direzione di osservazione e D il diametro del telescopio in cm. Si può abbattere aumentando il diametro dell'ottica e il tempo di integrazione, come mostrano i grafici a fianco.

La scintillazione è stata inserita nel segnale attraverso un numero random, con la seguente funzione:

Rreal = R(1+Pr x random); Breal = B(1+Pb x random)

in cui Pr e Pb sono rispettivamente l'incidenza che ha la scintillazione sul segnale: si è preso il 6% e l'8%; la diversità nei valori introduce il comportamento cromatico della scintillazione, che non è eliminabile attraverso la misura differenziale.

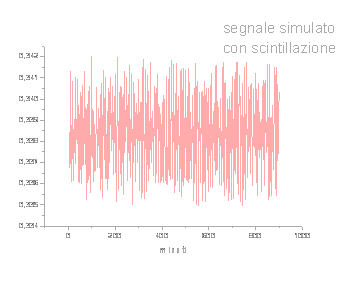
La serie temporale reale così ottenuta è quella  rappresentata a fianco.

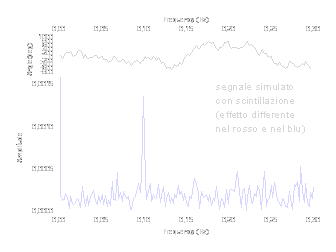
In ultimo se ne è calcolata la trasformata di Fourier (FFT). Il picco corrisponde esattamente alla frequenza impostata. Si può notare uno spettro approssimativamente piatto nel resto del tracciato, per effetto della scintillazione. Il picco è molto stretto, questo perchè la risoluzione in frequenza è molto alta, avendo una serie temporale con 90 cicli di oscillazione (simulati).